머신런의 기본이 되는 단층 퍼셉트론을 통계의 중선형회귀와 관련지어 이해해 보았다.
1. 단층 퍼셉트론과 중선형 회귀
중선형 회귀란 서로 다른 여러개의 특징을 독립변수로 하는 회귀의 결과를 판단하는 모형을 만드는 것이다.
가장 계산이 쉬운 단순선형회귀는 1개의 입력 특성으로 결과를 판단하는 것이고, 중선형회귀는 복수의 입력
특성을 통해 최종 적합을 출력하는 선형회귀이다.
예를 들어 나이에 따른 혈압을 계산하는 것이 단순선형회귀라면, 나이와 몸무게를 입력으로 혈압을 추정하는
것이 중선형 회귀이다. ( 이러한 수치 계산은 통계 Tool인 R을 이용하여 비교적 간편하게 수행할수 있다 )
이를 확장하여 분류에 적용한다고 하자. 몸무게, 키등 연산이 가능한 수치값을 입력 변수로 하여 범주형 변수
(수치로 계산이 불가한)인 비만 여부를 판단한다고 할때, 이렇게 분류의 범위로 중선형회귀를 확장한 것은
R로 작업하기에 용이하지 않으며 (물론 불가능은 아닌것 같다) 머신런을 통해 작업하면 보다 쉽게 결과를
도출할수 있고 시각화가 용이하다.
다수의 특성을 입력값(통계에서의 독립변수)으로 단순 범주형 결과를 얻기 위해서는 머신런의 가장 기본적인
구조인 단층 퍼셉트론을 활용할수 있다. 다만, 입력층과 출력층으로 구성된 단층의 Feedforward 신경망
구조이므로 단층으로 구성되어 하나의 선형 경계만 학습할수 있으므로 0과 1의 두가지 종류의 출력만 가능하다.
( 단, 두개의 명목형 변수를 구분하기 위한 분류에만 적용할 수 있다 )
2. 단순선형회귀와 중선형회귀
이러한 학습의 기본 원리가 되는 단순선형회귀에 대한 이론적인 근거와 중선형 회귀로의확장은 아래와 같다.
(1)단순선형회귀
중선형 회귀를 이해하기 위해 우선 단순선형회귀 (1개의 연속형 입력값으로 1개의 연속형값을
설명하는 회귀 )를 살펴보면 아래와 같다. 단순선형회귀는 하나의 직선으로 데이터를 설명하는 것으로
독립변수 X에 대한 Y의 기대값이 E(X|Y)= 𝜷₀ + 𝜷₁X, 데이터를 잘 설명하는 𝜷₀, 𝜷₁ 을 찾는것이다.
기대값과 출력값의 차이(잔차)를 이용한 최소제곱법을 사용하며, 잔차의 제곱합을 최소화하면서
적절한 계수를 찾아낸다.

** 잔차를 이용한 분석에서는 오차의 독립성, 등분산성, 정규분포에 대한 가정이 우선함
통계에서는 회귀직선이 예측하는 반응변수(결과)의 값과 실 반응변수의 관측값이 가까울수록(잔차가 작을수록)
회귀직선이 데이터를 잘 설명한다고 판단한다. 잔차의 크고 작음을 판단하기 위해서는 데이터 전체의 변동과
비교해서 관찰하며, 제곱합을 정의해서 회귀직선의 적합도를 평한다. ( 통계에서 결정 계수는 0과 1사이의
값으로 0이면 회귀직선이 데이터를 설명하지 못함, 1이면 데이터를 완벽하게 설명한다고 판단한다 )
머신런에서는 이러한 잔차를 최소화하도록 가중치를(𝜷) 조정하며 여러번의 반복학습을 통해 최적화한다.

(2) 중선형회귀
중선형 회귀는 독립변수의 종류가 2개 이상인 선형회귀모형이다. 여러개의 연속형 변인에 연속형 결과값을
추정하는 경우는 선형회귀관련 모형을 R을 이용해 간단히 계산할수 있다.
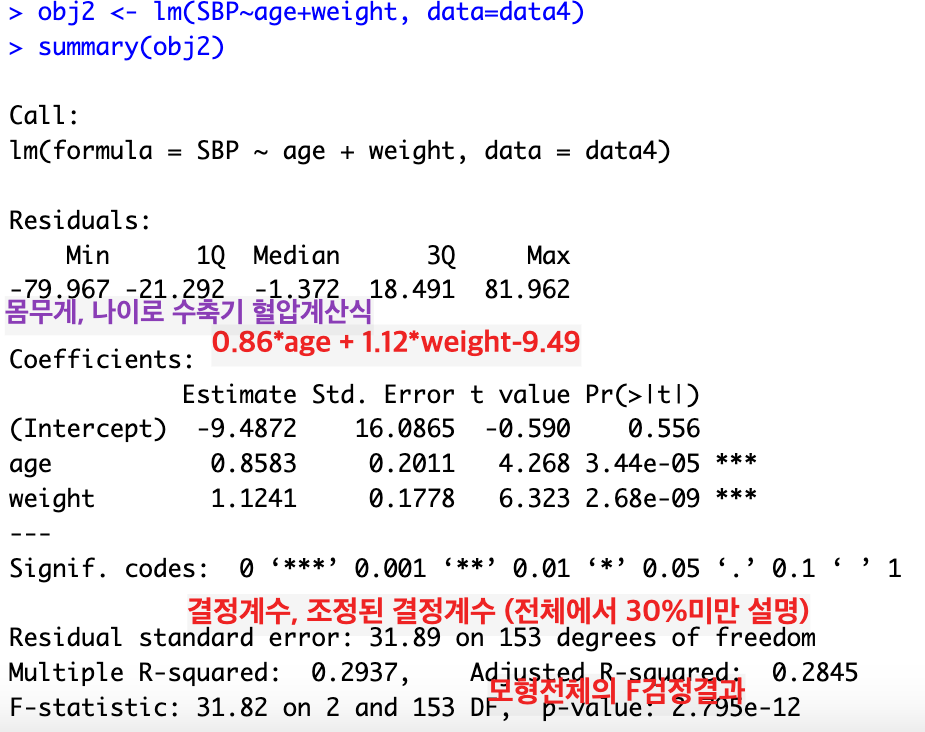
예를 들어, 나이(age)와 몸무게(weight)에 따른 수축기 혈압(SBP)계산은 0.86*나이+1.12*몸무게 - 9.49
이다. 이는 아래와 같이 R을 이용한 계산결과이다.
만약, 다수의 연속형 독립변수로서 수치가 아닌 범주형 결과변수를 판단하는 경우( 예를 들어 키, 몸무게
등의 수치값으로 비만 등의 명목형 변수를 판단 ) 다중 로지스틱 회귀를 사용하게 된다.
다중 로지스틱 회귀는 1개의 case에 여러 특성의 입력값을 가지고 있으며, 각 특성별 가중치를 합한 후
비선형 특성을 가지는 활성 함수를 사용하여 출력 여부를 결정한다.
신경세포의 원리를 모방하여 특정 임계값을 기준으로 출력이 결정되는데, 아래의 Fig.2에 나타난 바와
같이 𝑢의 값이 0보다 작으면 출력을 억제하고, 0보다 크면 출력을 내도록 설계된다.
바이어스(bias)로 뉴런이 활성화되는 𝝎ᵀх의 레벨을 조정한다.
이러한 다중로지스틱 회귀를 머신런에 적용하여 출력값을 결정할 때는 모델의 특성에 따라 다양한 활성
함수( Step function , Sigmoid Function, ReLU , Leaky ReLU등)를 사용한다.
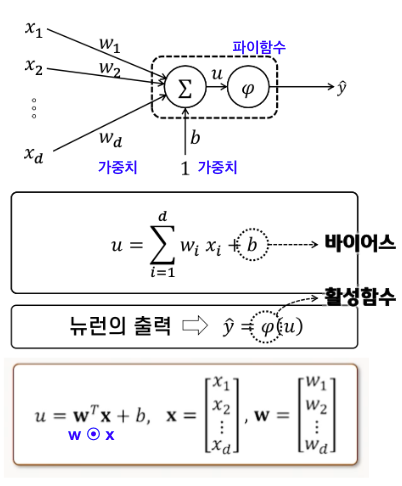
Fig.2 d개의 특성에 대해 출력을 판단
위와같이 범주 분류를 위한 로지스틱 회귀는 R등의 통계 Tool을 이용해 간편히 수행할 수 없으며,
머신런을 통해 작업하면 보다 쉽게 결과를 도출할수 있고 시각화도 용이하다.
3. Single Layer Perceptron 구성 코드 실습( 구글 CoLab사용 )
Fisher의 붓꽃 데이터 집합을 사용하여 setosa, virginica, versicolor의 3가지 종의 붓꽃중 1가지를
target으로 잡아 예측하는 모형을 구축한다. ( 교과의 딥런 첫장의 코드를 구현했다 )
단층 퍼셉트론을 이용하면 두가지의 구분만 가능하므로 target과 나머지(1과 0)으로 구분한다.
붗꽃종의 구분을 위한 특징값(통계학의 독립변수)는 여러개를 사용할수 있으나 여기에서는 단순하게 꽃잎의
길이와 폭만 사용한다. ( Rosenblatt의 논문에서는 단층 퍼셉트론은 활성함수로 step-function을 사용하며
이를 그대로 적용) 이러한 학습을 통해 target품종의 꽃잎의 길이와 폭을 학습하여 타 품종과의 결정경계를
분명히 하며, 꽃잎의 길이의 폭에 대한 새로운 데이터가 입력된다면 target품종인지에 대한 예측이 가능하다.
실습 : 싸이킷런의 Iris데이터를 이용하여 특정 붗꽃의 분류 영역을 구분 (150개 데이터집합)
방법 : Single-layer perceptron구현, step-function
독립변수 2가지 - 꽃잎의 길이, 꽃잎의 폭
결과변수 - setosa, verginica, versicolor 중 1가지 target (target과 나머지로 구분)
최종결과 : 꽃잎의 길이와 폭에 대해 target으로 분류하는 결정경계 학습




출력결과 :

위와 같이 magenta와 blue의 dot형태로 주어진 학습 데이터를 표시하였으며,
이를 통해 학습된 결과로서 target품종(setosa)으로 예측될수 있는 범위와 타 품종의
예측범위를 구분하여 좌표계 내 영역으로 나타내었다.
** 학습중에 이해한 내용을 작성한 것이므로 내용이 혹 이론과 다르거나 잘못되었을 수 있습니다.
댓글 주시면 좀 더 깊이있게 이해하여 심화해보겠습니다.
'growth-log' 카테고리의 다른 글
| Youtube 데이터 크롤링 (3) | 2024.10.12 |
|---|---|
| 심층 합성곱 신경망_ AlexaNet과 VGGNet16 (0) | 2024.09.28 |
| 피그마 인터액션 (0) | 2024.08.29 |
| 피그마_페이지의 기본 스타일 설정 (0) | 2024.08.10 |
| Visitor 패턴 (0) | 2024.07.28 |


